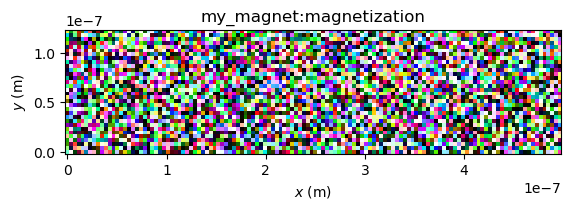
Micromagnetic standard problem #4

The problem specification can be found here.

from mumaxplus import *
from mumaxplus.util import show_field

import matplotlib.pyplot as plt
import numpy as np

Construct a world containing a single magnet with the dimensions mentioned in the problem specification.

length, width, thickness = 500e-9, 125e-9, 3e-9
nx, ny, nz = 128, 32, 1

world = World(cellsize=(length/nx, width/ny, thickness/nz))

magnet = Ferromagnet(world, Grid((nx, ny, nz)), name="my_magnet")

magnet.msat = 800e3
magnet.aex = 13e-12
magnet.alpha = 0.02

show_field(magnet.magnetization)

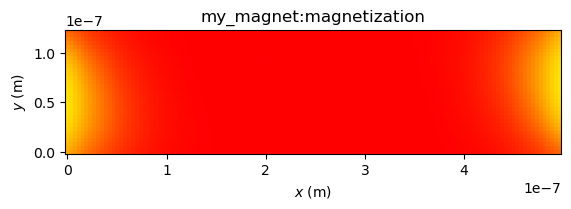
Relax the magnetization to an ‘S’ state in the x-direction.

magnet.magnetization = (1, 0.1, 0)
magnet.minimize()

show_field(magnet.magnetization)

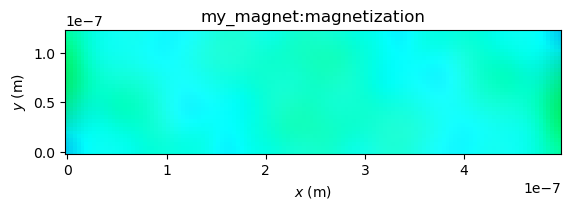
Apply one of the two external fields mentioned in the problem specification.

world.bias_magnetic_field = (-24.6e-3, 4.3e-3, 0)
#world.bias_magnetic_field = (-35.5e-3, -6.3e-3, 0)

Schedule the output by defining a list of timepoints and a table of quantities.

timepoints = np.linspace(0, 1e-9, 200)
outputquantities = {
    "mx": lambda: magnet.magnetization.average()[0],
    "my": lambda: magnet.magnetization.average()[1],
    "mz": lambda: magnet.magnetization.average()[2],
    "e_total": magnet.total_energy,
    "e_exchange": magnet.exchange_energy,
    "e_zeeman": magnet.zeeman_energy,
    "e_demag": magnet.demag_energy
}

Run a timesolver to evaluate the table quantities at the given time points.

output = world.timesolver.solve(timepoints, outputquantities)

show_field(magnet.magnetization)

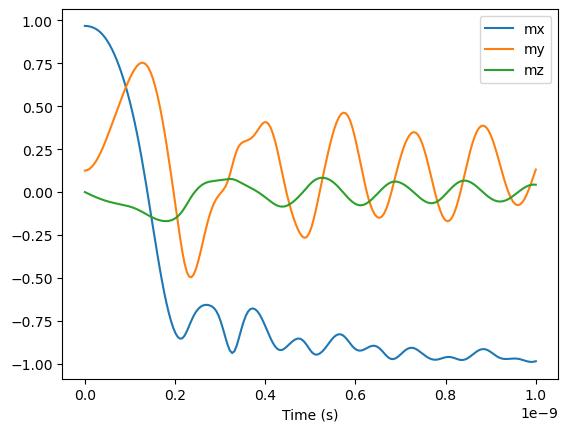
Plot the average magnetization in time.

for key in ["mx", "my", "mz"]:
plt.plot(timepoints, output[key], label=key)

plt.xlabel("Time (s)")
plt.legend()
plt.show()

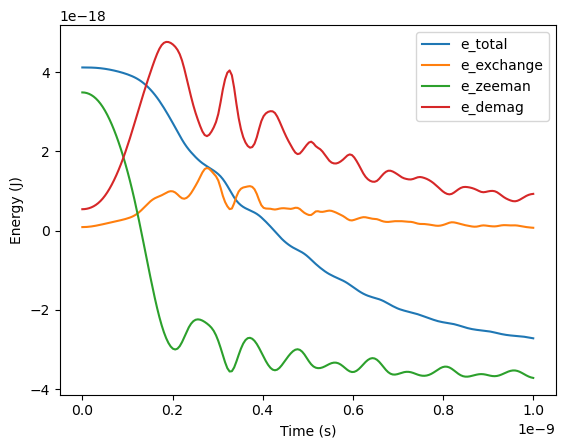
Plot the average energies.

for key in ["e_total", "e_exchange", "e_zeeman", "e_demag"]:
plt.plot(timepoints, output[key], label=key)

plt.xlabel("Time (s)")
plt.ylabel("Energy (J)")
plt.legend()
plt.show()