Voronoi#
This script shows how to use mumax⁺’s Voronoi Tesselator. This is inspired by figure 19 of the paper The design and verification of MuMax3.
import matplotlib.pyplot as plt
import numpy as np
from mumaxplus import Ferromagnet, Grid, World
from mumaxplus.util import Circle, VoronoiTessellator, vortex, plot_field, show_regions
# Set up simulation parameters
N = 256
c = 4e-9
d = 40e-9
world = World(cellsize=(c, c, d))
grid = Grid((N, N, 1))
# Create a circle
diam = N*c
geo = Circle(diam).translate(diam/2, diam/2, 0)
# Initialize a Voronoi Tesselator using a grainsize of 40e-9 m
tessellator = VoronoiTessellator(40e-9)
regions = tessellator.generate(world, grid)
# Create Ferromagnet
magnet = Ferromagnet(world, grid, geometry=geo, regions=regions)
magnet.alpha = 3
magnet.aex = 13e-12
magnet.msat = 860e3
# Set vortex magnetization
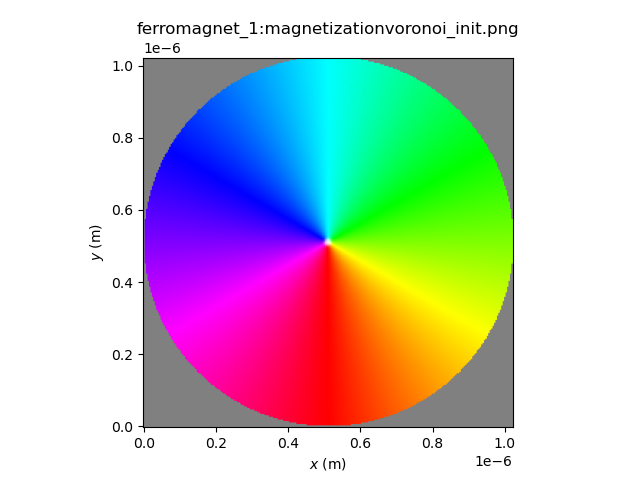
magnet.magnetization = vortex(magnet.center, 2*c, 1, 1)
plot_field(magnet.magnetization)
for i in tessellator.indices:
# Set random anisotropy axes in each region
anisC1 = tuple(np.random.normal(size=3))
anisC2 = tuple(np.random.normal(size=3))
magnet.anisC1.set_in_region(i, anisC1)
magnet.anisC2.set_in_region(i, anisC2)
# Create a random 10% anisotropy variation
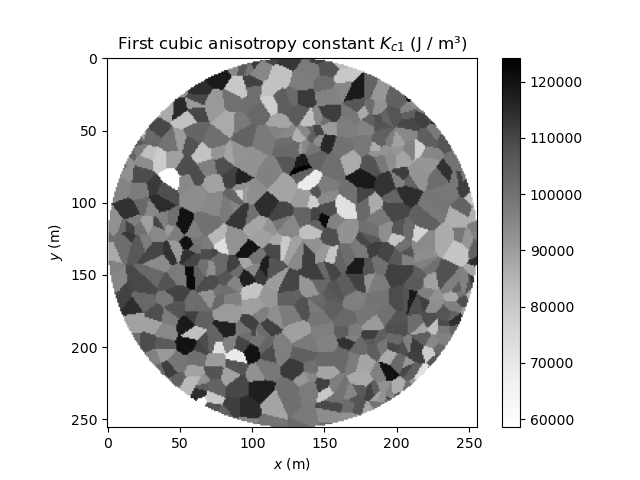
K = 1e5
magnet.kc1.set_in_region(i, K + np.random.normal() * 0.1 * K)
# Vary interregion aex
magnet.scale_exchange = 0.9
# Evolve the world in time
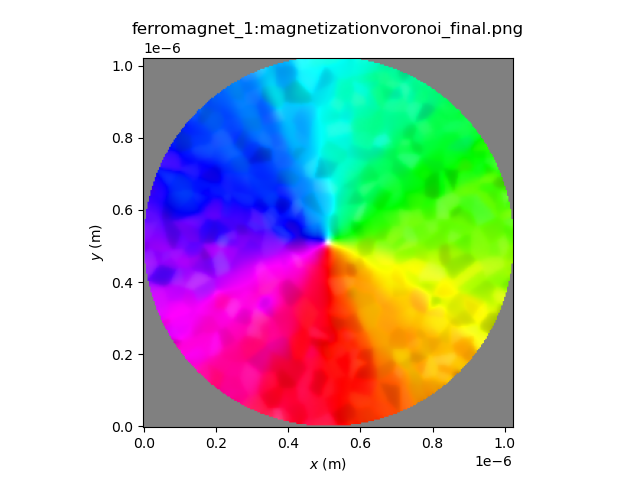
world.timesolver.run(0.1e-9)
plot_field(magnet.magnetization)
plot_field(magnet.kc1, imshow_kwargs={"cmap": "Greys"}, enable_colorbar=False)
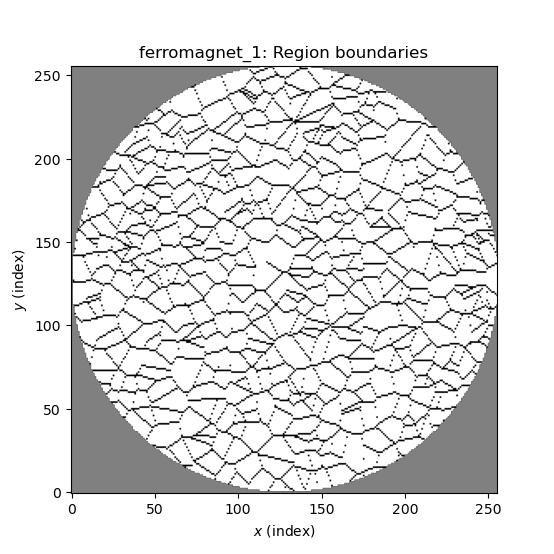
show_regions(magnet, geometry=magnet.geometry, imshow_kwargs={"cmap":"Greys"})