Standard Problem #2

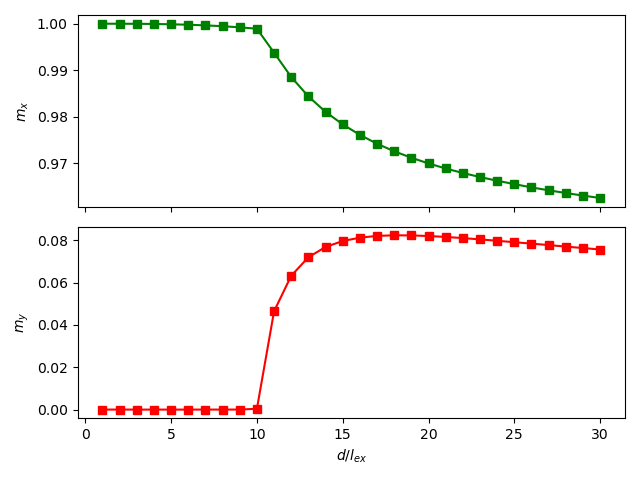
In standard problem 2 we look at the magnetization in function of the thickness devided by the exchange length.

import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm  # progress bar

from mumaxplus import Ferromagnet, Grid, World
from mumaxplus.util.constants import MU0

# dimensions
d_min, d_max, d_step = 1, 30, 1  # dimensionless widths d = width/l_ex
# maybe lower d_max when calculating coercivity
d_array = np.arange(d_min, d_max + 0.5*d_step, d_step)
t_p_d = 0.1  # thickness/width ratio
L_p_d = 5.0  # length/width ratio

# taking realistic parameters, but does not matter
msat = 800e3
aex = 13e-12
l_ex = np.sqrt(2*aex / (MU0 * msat**2))

def get_next_power_of_2(x):
    y = 1
    while y < x:
        y *= 2
    return y

def get_gridsize(L, d, t, l_ex=l_ex):
    """Cell length should at least be < l_ex/2. The number of cells is best
    a power of 2 for FFT. This results in cell sizes between 0.25*l_ex and
    0.5*l_ex."""
    return (get_next_power_of_2(2*L), get_next_power_of_2(2*d), get_next_power_of_2(2*t))

mx_list, my_list = [], []
rHc_list = []
for d in tqdm(d_array):
    L = L_p_d * d  # dimensionless length L = length/l_ex
    t = t_p_d * d  # dimensionless thickness t = thickness/l_ex

    nx, ny, nz = get_gridsize(L, d, t, l_ex=l_ex)
    world = World(cellsize=(L*l_ex/nx, d*l_ex/ny, t*l_ex/nz))
    magnet = Ferromagnet(world, Grid((nx, ny, nz)))
    magnet.msat = msat
    magnet.aex = aex

    magnet.magnetization = (1, 1, 1)  # fully saturated in specified direction
    magnet.minimize()  # TODO: try relax

    m = magnet.magnetization.average()  # remnance magnetization
    mx_list.append(m[0])
    my_list.append(m[1])

# --- Plotting ---

# remnance magnetization
fig, axs = plt.subplots(nrows=2, sharex="all")
mx_ax, my_ax = axs
mx_ax.plot(d_array, mx_list, marker="s", c="g")
my_ax.plot(d_array, my_list, marker="s", c="r")
mx_ax.set_ylabel("$m_x$")
my_ax.set_ylabel("$m_y$")
my_ax.set_xlabel("$d/l_{ex}$")

plt.tight_layout()
plt.show()